Conservation of Momentum - 2 Mass Inelastic Collision - Center of Mass Technique

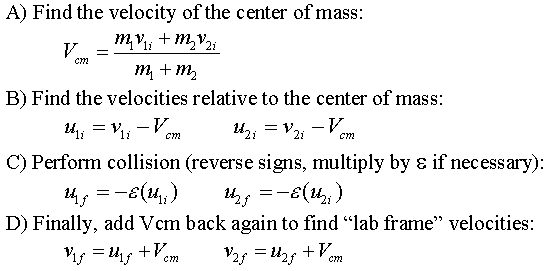
Description
There are two masses that can collide inelastically - you can adjust the coefficient of restitution from 0 (completely inelastic - they stick together) to 1 (completely elastic - bounce apart, and conserve KE). You can specify the initial velocities and masses for each mass, and the coefficient of restitution. (The arrow buttons near the initial values will double or half the values. If you manually change a value {not using the arrows}, click the UPDATE button.)
   Center of Mass view : This applet adds a view in the center of mass frame. The initial relative velocities are found by subtracting the Vcm from each mass's velocity. To perform the collision, we reverse the sign of the initial relative velocity, and multiply by the coefficient of restitution - this will give the relative velocity after the collision (notice if the coefficient is zero .. there is no relative velocity afterward .. and thus they are stuck together at the center of mass!). We could then add the Vcm to the final relative velocities to get the final lab frame velocities. Also, watch the white "X" that is moving in the black rectangle underneath the two masses in the lab frame .. that is the location of the center of mass of the two masses (it should have a constant velocity). The bottom center of mass frame is what you would see if you traveled along with that white X and looked at the motion of the masses relative to your position. Those relative velocities can be found with the following steps illustrated below :

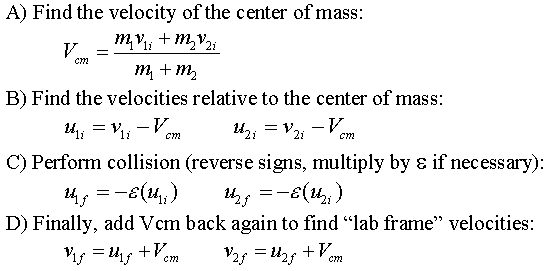
Some things to notice as you watch the collisions in the lab frame (top) and the center of mass frame (bottom) :

• The collisions occur simultaneously (we are just changing the "views" of the collision).
• The point where they collide changes in the lab frame (to the left or to the right, depending on initial conditions).
• The point where they collide does NOT change in the CM frame (it is always the origin of the frame .. by definition!).
• In the CM frame, with an elastic collision (e=1), the relative velocities before and after are the same for each mass (equal in magnitude and opposite in direction).
• In the CM frame, the momentum coming in from the left is always equal to the momentum coming in from the right (and its the same going out again). ... by definition!
• If you add the Vcm to the initial relative velocity in the CM frame, you would get the initial velocity in the lab frame.
• If you add the Vcm to the final relative velocity in the CM frame, you would get the final velocity in the lab frame.

Related Physlets :
       Conservation of Momentum - Energy to Separate (momenta1)
       Setting the Explosion energy between two masses (momenta2e)
       Conservation of Momentum - 2 Mass Elastic Collision (momenta3)
       Conservation of Momentum - 2 Mass Inelastic Collision (momenta3c)
       Conservation of Momentum - 2 Mass Inelastic Collision - Center of Mass Technique (momenta4)

Of the 863 visitors, you are the most recent!