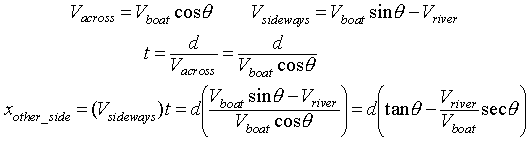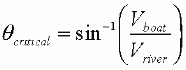The Physics behind BOATRIVER2
Moving a boat across a river is basically a "relative velocity"
problem in two directions. We start with the following assumptions to
orient ourselves (note : essentially, we are picking our coordinate system
- we can pick it any way we want, we just need to be consistant for the
rest of the problem) :
|
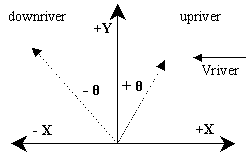
What coordinate system are we using?
- The boat speed and river speed are constant (and the river flows
East to West (Right to Left) in our example).
- We will start the boat on the South side of the river.
- The "line" between the starting dock and the dock
straight across will be our "theta = 0" line.
- We will measure the angle THETA as positive for pointing
upstream (to the East of North), and negative for downstream
(West of North).
- Let's consider the +X direction to be East and -X direction to be
West.
- Let's consider the +Y direction to be North (we don't need -Y
here).
|
|
What are the equations for the motion of the boat?
The boat will move sideways in the riverbased on the river's speed,
as well as any X component of the Boat speed. The boat will move across
the river based only on the Y component of the Boat speed. To find the
time for the boat to get to the other side, the y component of the boat
velocity, and the distance across are used. To find the distance along the
bank (measured from the point opposite your starting point), use the net
velocity sideways, and the time across. The equations are shown below :
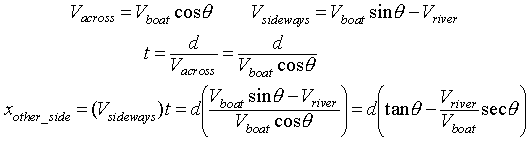
What can we measure from the Physlet?
The physlet tells us that the distance across the river is 3.5
meters (small river, huh?) - but we could also measure that (click the
mouse down on the far bank, the yellow box with the coordinates pops up in
the lower left corner .. they are x,y coordinates, so the second number,
y, should be 3.5 meters). If there is a particular point on the bank, we
could measure that x distance along the shore.
"Playing" is fine, but can you pre-calculate where you
will land if you know the angle?
YES! Looking at the equations above, if you have the boat velocity,
the river velocity, the distance across, and the angle, then the
equations above are easy.
What if you want to get to a particular point - can we calculate the
angle?
It depends ... if the boat velocity is greater than the
river velocity, then it is possible to get to any point on the far
side (upstream or downstream), but it involves solving the x(other_side)
equation above - not easy. Maple can do that, and here is
a worksheet to help you solve for
those angles. If the boat velocity is less than the river
velocity, then you are limited in how far you can reach on the other
side - and it will be some distance downstream from the point straight
across! The above Maple worksheet will work out that maximum x vlaue, or
you can look at this other Maple
worksheet that draws a graph of the distance vs the angle (so you
can see where the minimum is). Also, here is an
excel worksheet that draws the distance
vs angle graph. Essentially, the critical angle, for the case when
vb<vr :
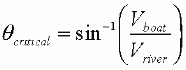
You could calculate that critical angle, and then plug that into the
x_other_side equation above to see where you would end up ... and that
would be the highest point upstream that you could reach (note: that point
will always be "downstream" from the point straight across the
river). [Notice also that if vb>vr, this equation no longer gives a
correct answer.]
Go back to the boat on the
river physlet!
565
visitors.