Introduction: Vernal Equinox (First day of Spring) ... ah, the time of the year when length-of-day=length-of-night=12 hours, right? Well, sort of ... the Vernal Equinox is the moment when the GEOMETRIC center of the Sun rises/sets. But, we calculate (and name) the sunrise as when the upper tip of the Sun comes up above the horizon , and the sunset when the last bit of the Sun dips below the horizon. By the time the equinox has arrived, we have already passed the 12 hour day mark! {Thus, it is true that the Northern and Southern hemispheres are equally illuminated on the Equinox, but because we count "day" as being from the very beginning of the sun-rising to the very end of the sun-setting ... we have more than 12 hours of daylight before the Equinox.}
A light bulb goes off: So, armed with that basic idea .. can I leave well enough alone? ... of course not! I got to thinking about when (in time) the moment of 12 hours occurs for us in Detroit .. wait, why not north or south of us .. and, while I'm at it, why not figure out the length of the day for every day of the year, for every latitude on the Earth (hey, you started it .. wait, I started it ... nevermind).
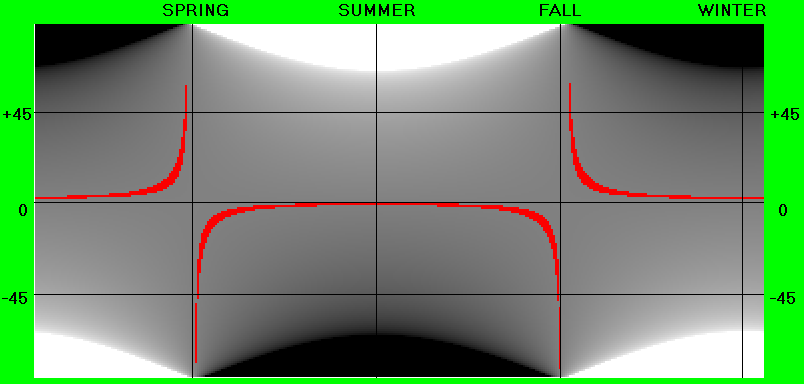
Fruits of my labor: Let's look at a fancy image illustrating many hours of head-scratching programming, and then I'll explain it.

Axes definitions: Ok, the vertical axis is the latitude on the Earth (postive above the equator, negative below the equator), so the North pole is the top of the image, and the South pole is the bottom of the image. The horizontal axis shows the days of the year, starting with Jan 1st, 2005 (with the Equinoxes and Solstices indicated). {Note: Since I'm writing this in the Northern Hemisphere .. when I say Summer, I mean July .. when I say Winter, I mean December, etc.}
Color codes: If it is black - that means there is no sun above the horizon all day (perpetual night). Notice that occurs near the South Pole (below -60) during July (South pole has "winter", North pole has "summer"). If it is white, that means the Sun is above the horizon the whole day (perpetual day). Notice this occurs for the North pole in July (northern hemisphere "summer"). If it is grey, it is somewhere in between 24 hours of light and 0 hours of light. The red marks indicate where the 12 hour cutoff is.
Check with Northern Hemisphere: So, let's make sure everything makes sense .. let's start in the upper left corner - that would be Northern Hemisphere in Jan .. short days (go too far north and you have no day!) - up to the red boundary of the 12 hours of daylight .. then moving right we cross over that red boundary into the long days of summer (notice the north pole has 24 hours of daylight). Then we hit the 12 hours on the way down, and then go to the short days of Winter. As we made those transitions ... notice that the red boundary was hit BEFORE the moment of Spring, and then when it is the Fall Equinox, we still have more that 12 hours .. until a few days AFTER the Fall equinox until we go into the shorter days of winter.
What about near the Equator? As we start moving toward the equator, notice that the 12 hour line is moving earlier and earlier in the year {or later and later in the Fall} .. and then goes off the scale? Hey, something weird is going on .. oh, wait, now I see ... at the equator, the time of the day is always longer than 12 hours every day of the year (but, not by much: it only varies from about 12 hours 4 minutes to 12 hours 10 minutes throughout the year!). So, the Equator can't really lay claim to the "long days of summer" - it is only 6 minutes longer than a winter day!
Southern Hemisphere: This is the "mirror image" of the North ... starts in Jan with long days .. goes past the Spring Equinox to get to the 12 hour day - then the short days (or no days at the South pole) when the North has long days, etc. [Notice the red sections "bracket" the black no-day areas .. both in the North and the South - so the effect is symmetric, as expected.]
Conclusion: Yes, the Equinoxes (and Solstices) are astronomically significant, but because we have defined our sunrise and sunset times in a particular way, the "equal day / equal night" situation is a little more complicated than it initially appears to be! Now I have to go calculate the probability of eggs standing on end on the Equinox ...
How did Dr. Scott make those calculations? Using some free software found on the internet (Author: Kambiz R. Khojasteh - website for Delphi programs : http://www.delphiarea.com/products/). That library routine was based in part on algorithms from Jean Meeus's book "Astronomical Algorithms" (he is an astronomical god!). I used the functions to generate the above graph in Delphi (and a data table was loaded into Excel for reference).
Return to the Astronomy Main Page
Of the 513 visitors so far, you are the most recent!