Consider a driven damped mass on a spring system. You can vary the driving frequency relative to the natural frequency, you can also vary the damping relative to the natural freqency. The driving force will be given as a step function, with the portion of the period that the force is active being variable (DT/T). Consider the image below:

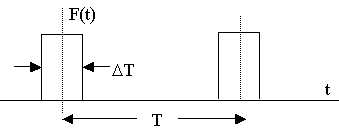
The step-function driving force can be approximated as a Fourier sine series, which will lead to a sine series as a response function:

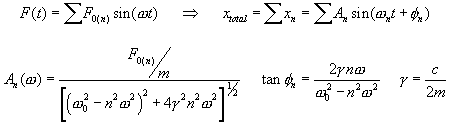
Vary the driving freqency, the damping effect, and the number of terms of the sine series to investigate the various effects on the response function.