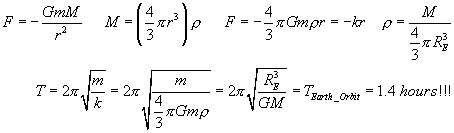
Drop through the Earth .. or orbit it .. so many decisions!Dig a hole through the center of the Earth? Well, first .. we can't! Forget the fact that we have a mostly molten core ... we have barely gone a few miles down into the crust! Plus, the physics we are going to talk about here won't work with a rotating Earth (or at least not the way we plan to analyze it). So that means we have to stop the rotation of the Earth .. and we saw Superman do that in the movies, and he stopped time - then we have to reset all our clocks .. what a hassle. So, let's start with a non-rotating, easily cored planet. If you dug a hole straight through ... and dropped in, from rest, you would undergo Simple Harmonic Motion as you fell down, passed through the core, and rose out to the other side. (Essentially, the Earth appears to be a giant "spring" with an appropriate spring constant). Based on our simple harmonic motion studies, we can calculate the maximum speed you would reach (naturally, that would be at the exact center) ... and lo and behold, it is exactly the same as the speed you would need to orbit the Earth at the surface of the Earth (the Bugs Bunny Baseball speed). But wait ... if the object dropping through the core only reaches a MAXIMUM speed of the orbit speed .. and the orbiting object ALWAYS has that speed ... if Bugs dropped one baseball, and threw the other one into orbit .. which would come back first? Run the simulation to the right, and then see if you can explain why!! |
|
Here are the calculations to prove that the period of the SHM is the same as the period of the orbit at the Earth's radius:
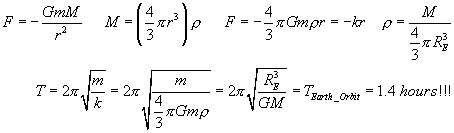
Write the gravitational force equation. Assume the particle is some distance out from the center of the Earth, then the "big mass" is the mass of the Earth closer to the origin - so use the density of the Earth, and the volume at that radius (r). This gives the "force vs distance" relationship for SHM! Using the "spring constant", and the period equation ... we find the period of that motion to be the same as if the object was orbiting the Earth at the Earth's surface. (Note, the period is independent of the distance out from the center .. so suppose you climbed down to halfway through the Earth, and dropped from there ... it would still take you the 1.4 hours to go to the other side (halfway out), and come back ... in fact, go to the center, jump outward .. you would travel about 1 km in that first jump, and then fall back, go past the center .. then come back again .. all in that same 1.4 hours!