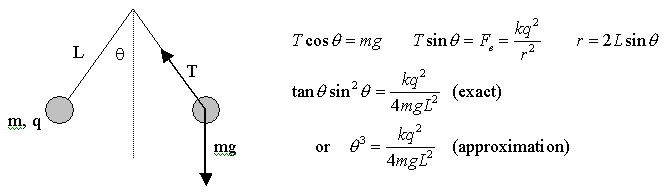
This physlet illustrates a dynamic method to find the answer to a complicated equation. In an electroscope problem (see explanation below physlet), if you have the angle, and need to find the charge required, it is quite easy to solve. But, if you have the charge, and need to figure out the angle - there is no closed form solution (but there is an approximate solution).
|
This physlet shows an intial
electroscope setup - you select the charges, the length of the string,
and the masses. The system will then calculate an angle based on the
approximation outlined below. It will set the angle for the
electroscope, and then "let it go". But, depending on the
quality of the approximation, the charges might not be in equilibrium,
so they will start to move (basically oscillate around the
equilibrum).
|
This is a model of a simple electroscope - the two "bobs" will separate from each other because they have like charges. The separation will depend on the length of the strings, the mass of the bobs, and how much charge is on the bobs. We can use simple forces to generate the equations we would need to model this system :
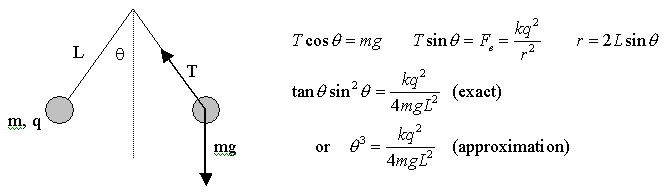
Now, to solve the exact equation, we would need to use something like MAPLE - there is no easy analytical solution. Here is a Maple worksheet that calculates this model, and let's you change values. (Right click on the link, and use the "save as" choice to copy the worksheet to your computer, then open it in Maple.)
In the animation above, there are two like-charged 500-gram spheres
attached to strings to form an electroscope (position given in centimeters
and time is in seconds). You may drag the spheres to whatever
position you wish before or during the animation. Now, initially, the
system will use the approximate angle to place the masses, based on the
choices you make to the right of the animation. For small angles, the
approximate initial angle is very good, so the system will essentially be
static (that is, it is the correct angle for equilibrium). But, if the
angle is big (such as if the length is small, and the charge is big) - the
approximate angle will be different enough from the exact angle, that the
system will "oscillate" a little. If this happens, you can damp
the motion by clicking the "Damp Velocity" button. (It will
temporarily stop the charges from moving .. as they get close to their
equilibrium points, periodically "damp" them, until they are
motionless .. thus, in equilibrium).
Reset using current values
Reset using original values when
you loaded the page
Credits: Physlet problem authored by Mario Belloni. Modified by Scott Schneider at LTU.