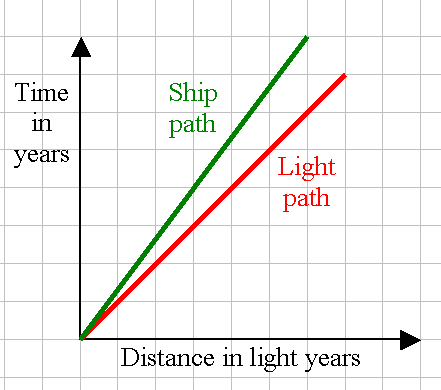
Minkowski diagrams can be very useful when dealing with events that occur in relativistic space-time. Here is a simple twin paradox example illustrated (and then extrapolated to a triplet paradox).
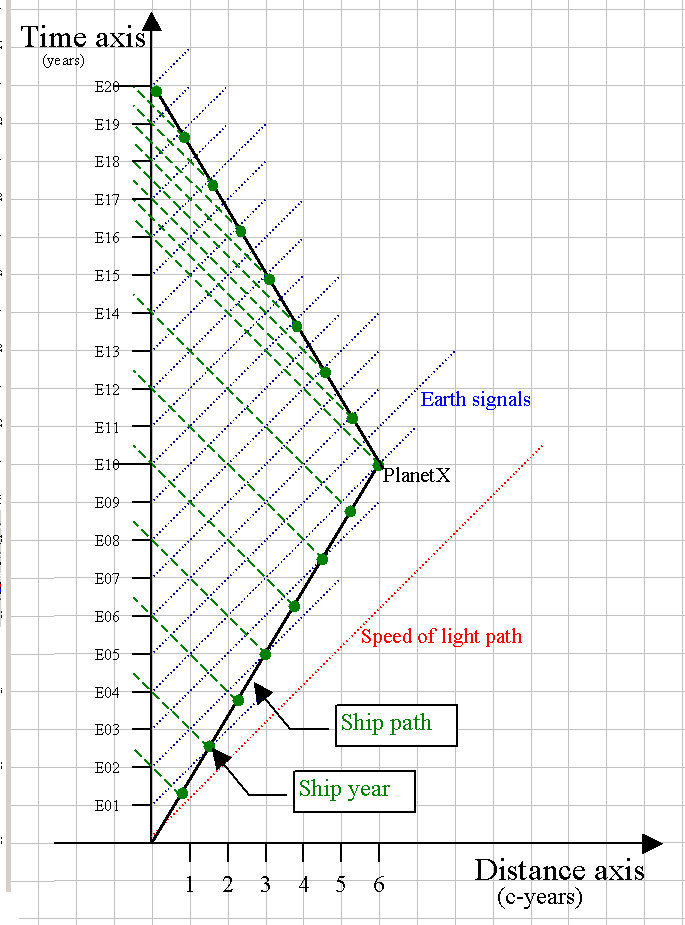
First, the Minkowski diagram graphs the distance traveled (by light or a spaceship) along the horizontal axis, and the Earth Time by the vertical axis. The units will be years for time and c-years for distance. In this diagram (with equal horizontal and vertical unit scales), a light path will be a 45 degree angle line, and a ship (moving slower than the speed of light) will travel with a larger angle slope (same distance, but more time, thus a lower speed than c). Here are samples of a light signal coming from the Earth at t=0 years, and a ship leaving at that same time (in this case, the speed looks to be 6/8 = 0.75 c):

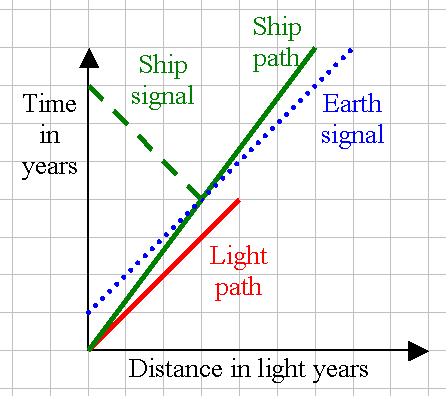
Once we have that diagram ... we could look at the twin paradox, and send signals from the Earth toward the ship (every Earth year) and then send a signal from the ship back to the Earth (every ship year). The signals from earth will be lines that are unit-slope lines (since they are light signals), and the signals from the ship will also be unit slope lines (but angled back toward the time axis, since they are heading back toward Earth). When Earth signal line hits the ship path, that Earth signal has been received by the ship. Likewise, when the ship signal hits the time axis, that means the Earth (which has moved "forward" in time, but not forward in distance) has received the signal. For example, look at the blue Earth signal - it leaves the Earth 1 year after the ship left - when will it catch up to the ship? Well, it looks like the ship is 3 c-years away - it took 4 earth years to get there at 0.75 c. The earth signal can cover 3 c-years in 3 years ... plus the 1 year delay = 4 earth years ... so the signal and the ship are now at the same location. What if the ship sent a signal back to the Earth at just that moment - how long will it take (total elapsed time) until the Earth receives that "bounce"? Well, the ship is 3 c-years away - so it will take three years for the signal to get back to the Earth ... thus a total of 7 years (notice the green dotted line intersects the time axis at 7 years).
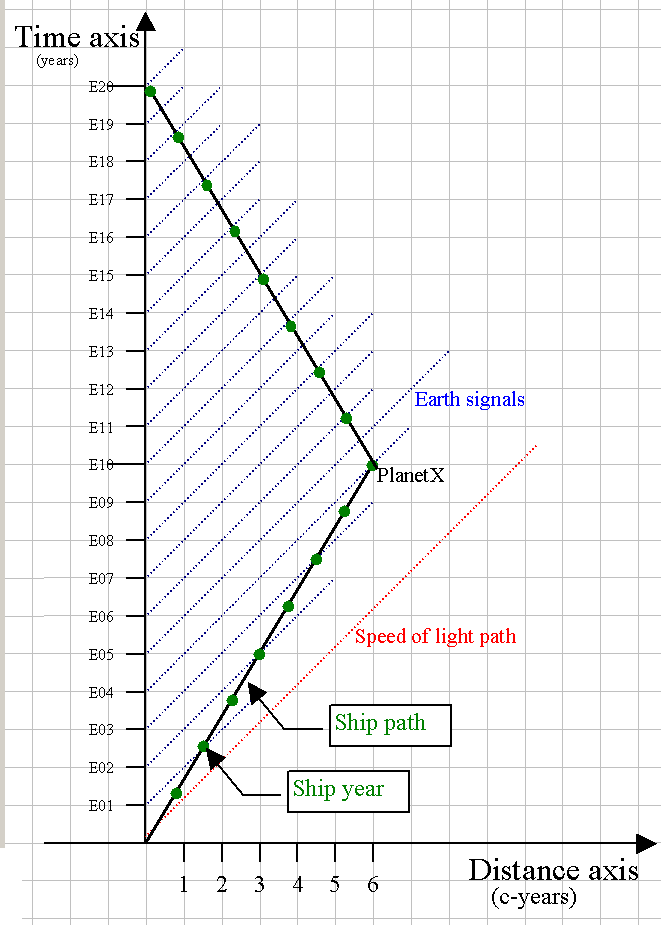
Ok, let's try a standard twin paradox example. There is a planet that is 6 c-years away from earth - and the ship can travel at 0.6c - so it will take 10 Earth years to get to the planet, and 10 years back (total time of 20 years elapsed on Earth). But, at that speed, the time dilation equations tell us that the ship will experience 8 years of time elapsed on the way out, and 8 years on the way back ... so 16 ship years, for 20 earth years. Let's count how many signals the ship receives from the Earth (notice the blue Earth signal lines are moving upward diagonally, spaced every 1 Earth year). Also, the green dots on the ship path are the ship year markers.
On the way out - for every 2 ship years, it gets one signal (this fits the relativisitic frequency shift for this speed - should be 1/2 signal rate). As soon as the ship turns around and heads back (now the ship path heads back toward the time axis) - the rate doubles to 2 earth signals per ship year. So, on the way out - (8)(1/2) = 4 Earth signals ... on the way back (8)(2) = 16 signals ... total = 20 Earth signals, as expected.
What if we turned it around, and looked at the ship sending out signals to the Earth. In this case, when the ship thinks a year has passed, it sends a signal to the Earth (green lines of unit slope - heading back toward the time). Notice when the ship heads toward the planet, the Earth receives that 1/2 rate. At the Earth's 10th year, the ship has technically arrived at the planet, but the signal has just left the planet, and will take 6 years to get back ... notice that for the Earth, the signal rate doesn't change until the "arrival signal" has gotten there. Only then does the rate double. So, to add up the time, (16)(1/2) = 8 signals until arrival - then (4)(2) = 8 signals .... thus 16 ship signals received by the Earth.
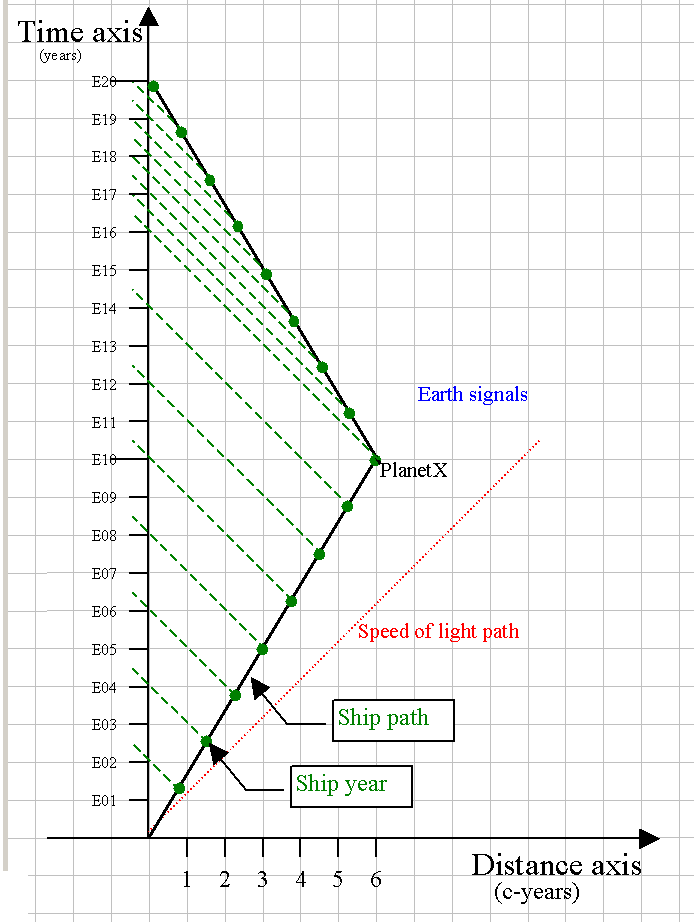
Let's put both pieces together (but then the graph gets more complicated).
Triplet paradox?
Now that we have looked at the twin paradox - what about having triplets - one stays on Earth, one goes out to planet X, and another goes in the opposite direction to planet Y. The next question is, what does Triplet X see as the speed of Triplet Y ... and what about signals from Triplet X getting to Triplet Y - how old will they see each other? [Based on the idea of the twin paradox. Triplet X and Triplet Y should be the same age, and younger than Triplet E (for Earth). But, as they move away from each other, they can't perceive the other's speed as being greater than the speed of light!]
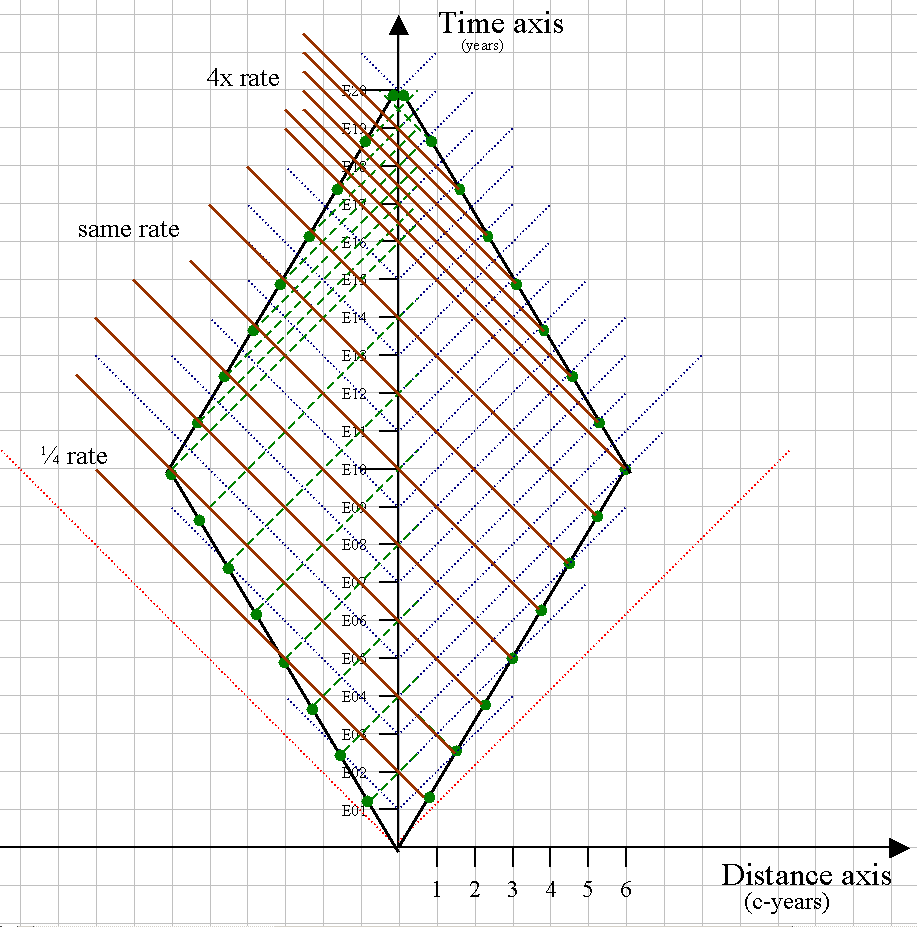
Let's do the math first, to get the numbers that will later show up on the graph. Let's assume we have the planets in a line. X, then 6 c-years later is Earth, then 6 c-years later is Y. The ships can move at 0.6c (as above), so the moving twins take 10 Earth years to get to their respective planets, and 10 years back. But for that 20 Earth year journey, the moving twins experience 16 ship years. And thus, if they send out signals to each other, they better receive 16 signals.
Now, what is the speed that Triplet X sees for the ship for Triplet Y? According to the relativisistic velocity addition formula, the speed would be 0.88235c (notice, classically, it would be 1.2 c = 0.6 + 0.6). What signal rates would the ships perceive from each other? If the ships are moving away, we get a 1/4 signal rate (every 4 ship years, you would receive 1 signal from the other ship). [Compare this to the Earth, every 2 years, they are receiving 1 ship signal.] If they are moving toward each other, the signal rate jumps to 4 times (4 signals for every ship year). [Compare to the Earth with the 2x rate.]
Let's look at how this works on the graph. For the new ship, we just mirror the above diagram around the time axis (so, one ship goes +x and one goes -x). The signals from the first ship can now reach the second ship and be counted. (To make the diagram a little less complicated, we are only showing the +x signals going to the -x ship.)
For the -x ship, the whole journey out, they only get 2 signals? Yes, this make sense, the ships are moving away, the frequency rate should be 1/4 ... so 8 ship years means 2 signals from the other ship. [At this point, both ships have arrived at their planets, but remember, the +x ship signals are still coming through space, and they are "separated" as though from the receeding ship.]
Once the -x ship turns around and heads back to the Earth - it starts getting a signal every ship year - is that right? Yes, the signals from the +x ship are separated in space as though the +x ship is receeding .. but now the -x ship is "approaching" those signals - so it is like the two ships are moving in the same direction, at the same speed - there shouldn't be a rate change .. so every ship year, the ship gets a signal from the other ship.
What happens when the -x ship finally gets the "arrival" signal (when the +x ship gets to the planet). Since the +x ship has now turned around and is sending out signals in front of it ... and since the -x ship is still heading back toward the Earth - the signal rate jumps to 4 times the rate ... so, for the last two -x ship years, they receive 8 signals from the other ship. (Note : I left off the second to last signal by mistake .. and then the last signal is when both ships reach the Earth.) Count up all the signals - 2 + 6 + 8 = 16 signals from +x ship ... and 16 years on the -x ship ... they match!!
[In the twin paradox, there are only two rates that are used - when the ship goes out, and when it comes back {but, note that the Earth observer and the ship observer see the rates changing at different points in time}. When we go to the triplets, we actually now have three rates ... the slower rate, the faster rate, and then the equal rate. This comes about because with two ships moving ... sometimes they (or their signals) are receeding {the slow rate}, sometimes they are approaching {the fast rate}, but sometimes they are arranged such that it looks like the ships are just chasing each other {so, the lead ship sends out signals that are rated down, but then the ship comes along and picks them up, which rates them up - and they balance out}.]
Now, don't even ask about the quintuplets ... sheesh, that is complicated!
Long ago and light years away ...